En este artículo se presenta una solución al reto EquationSolver (exp60) del InternetWache CTF 2016. Agradecemos a los organizadores por las muchas horas de diversión y aprendizaje que nos han regalado.

Descripción

El reto nos presenta la siguiente descripción:

I created a program for an unsolveable equation system. My friend somehow forced it to solve the equations. Can you tell me how he did it?

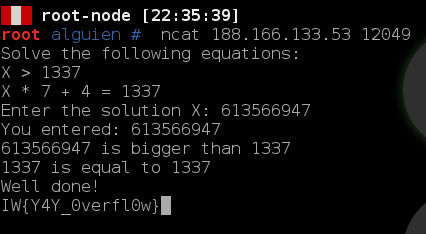
Además de una dirección IP y puerto donde luego de conectar con Netcat, vemos lo siguiente:

Solve the following equations:
X > 1337
X * 7 + 4 = 1337
Enter the solution X:

Análisis

El sistema de ecuaciones al que se refiere la descripción es: X > 1337 y X * 7 + 4 = 1337. Aparentemente es un sistema de ecuaciones que no tiene solución. Si X es mayor que 1337 ¿Cómo podría X * 7 + 4 ser igual a 1337?

Luego de un brainstorming en el chat de Amn3s1a, se sugirió provocar un integer overflow. Un integer overflow sucede cuando la representación binaria de un número no cabe en los 4 bytes de una variable tipo int. En tal caso los bits en exceso se truncan y son ignorados.

Veamos un ejemplo. En el siguiente código int x = 0xFFFFFFFF, y = x + 1; el valor de y quedaría en 0 puesto que 0xFFFFFFFF + 1 es 0x0100000000 y luego de truncarlo a 4 bytes queda 0x00000000 lo cual es ciertamente 0.

La idea es usar este comportamiento para resolver el sistema de ecuaciones.

Solución

Entonces debemos buscar un número X tal que X * 7 + 4 genere un integer overflow que resulte en 1337.

Expresandolo en forma de ecuación:

X * 7 + 4 = 1337
X * 7     = 1333

Operamos un poco para representar la ecuación X * 7 = 1333 de forma más conveniente:

X * 7       = 1333
X * 8 - X   = 1333
X * 2^3 - X = 1333    (2^3: 2 elevado al cubo)
X<<3 - X    = 1333    (X<<3: X desplazado 3 bits a la izquierda)

En la ecuación X<<3 - X = 1333 observamos 3 elementos:

• 1333 cuya representación binaria es 00000000 00000000 00000101 00110101
• X del cual no conocemos ningún bit y por ello lo representaré así ???????? ???????? ???????? ????????
• Y X<<3 que es X con un desplazamiento de 3 bits, es decir: ???????? ???????? ???????? ?????000

Ahora vamos a mostrar la ecuación X<<3 = 1333 + X de forma más familiar:

1333  =  00000000 00000000 00000101 00110101 +
   X  =  ???????? ???????? ???????? ????????
____     ___________________________________
X<<3  =  ???????? ???????? ???????? ?????000

Hemos reducido el problema a una suma de números en base 2. Ahora podemos deducir uno a uno los bits de X sumando por columnas como en la escuela. Por ejemplo: en la primera columna tenemos 1 + ? = 0 con lo cual deducimos que la interrogante debe valer 1 y se genera un acarreo de 1 para la suma de la siguiente columna.

                                          1  <----- acarreo
1333  =  00000000 00000000 00000101 00110101 +
   X  =  ???????? ???????? ???????? ???????1
____     ___________________________________
X<<3  =  ???????? ???????? ???????? ????1000

Y ya encontramos el primer bit de X.

Observe que como X<<3 es igual a X pero desplazado 3 bits a la izquierda, el primer bit de X es igual al cuarto bit de X<<3.

En la segunda columna tenemos 1 + 0 + ? = 0. Nuevamente la interrogante debe ser 1 y llevamos un acarreo de 1 para la siguiente operación.

                                         11  <----- acarreo
1333  =  00000000 00000000 00000101 00110101 +
   X  =  ???????? ???????? ???????? ??????11
____     ___________________________________
X<<3  =  ???????? ???????? ???????? ???11000

Continuamos de esta manera hasta hallar todos los bits de X. Finalmente obtenemos:

                                 11 11  111  <----- acarreo
1333  =  00000000 00000000 00000101 00110101 +
   X  =  00100100 10010010 01001001 11100011
____     ___________________________________
X<<3  =  00100100 10010010 01001111 00011000

Por último, pasando 00100100 10010010 01001001 11100011 a base decimal obtenemos 613566947.

Flag

FLAG: IW{Y4Y_0verfl0w}